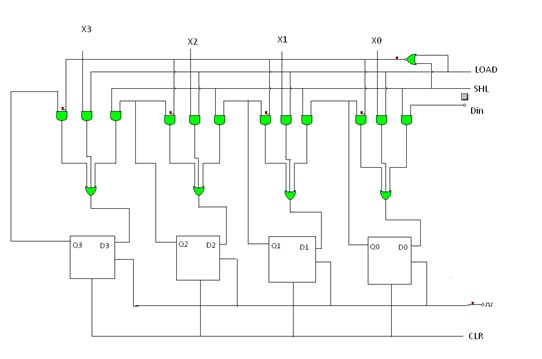
+.REGISTER GESER TERKENDALI(controlled shift register)
yaitu: rangkaian yang mempunyai masukan-masukan kendali yang mengatur operasi rangkaian pada pulsa pendetak
gambar rangkaian:
cara kerja / pengisian:
1. Pengisian Peralel atau serentak (parallel or broadside loading).
yaitu rangkaian yang dapat mengisikan demua bit secara bersamaan ke dalam flip-flop.,mirip dengan register buffer.
1. saat load dan shl=0 maka keluaran NOR adalah 1, lalu keluaran - keluaran flip - flop akan memberikan kembali masukan - masukan datanya.
2. saat load=0 dan shl =1, maka rangkaian akan (bertindak sebagai register kiriRegister Seri), yaitu semua inputn atau nilai di masukan dari Din dan nilai pertama akan bergeser kearah kiri. sampai semua bit terisi. Jadi pengisian di lakukan satu – persatu.
3. saat load=1, dan shl=0 ,rangkaian berfungsi sebagai register buffer karena semua bit X akan mamasuki flip-flop untuk pengisian parallel secara serentak. Yaitu :
-. saat load =0, maka nilai Q= C(tetap).
nilai LOAD masuk ke AND dan nilai keluarannya masuk lagi ke OR ,dan tergantung dari clk nya jika nilainya tinggi Q0 maka niali D0 nya ikut tinggi
-. saat load = 1 maka nilai Q = X
nilai LOAD masuk ke AND dan nilai keluarannya masuk lagi ke OR,ketika nilai dari AND nilainya sama dengan nilai X.
-. load dan shl tidak boleh tinggi serentak, kerena dua ragam operasi yang berbeda tidak mungkin dilaksanakan dengan sinyal detak tunggal.